If the return is $0.10, then \(x = 0.1\) (this is our observed value). Very high or very low (negative) z-scores, associated with very small p-values, are found in the tails of the normal distribution. The probability that the return is less than $1 is closest to: The returns on ABC stock are normally distributed, where the mean is $0.60 with a standard deviation of $0.20. Positive z-values Example: Using the z-score Table If X X is a normally distributed random variable and X N(, ) X N (, ), then the z -score is: z x (6.3.2) (6.3.2) z x.
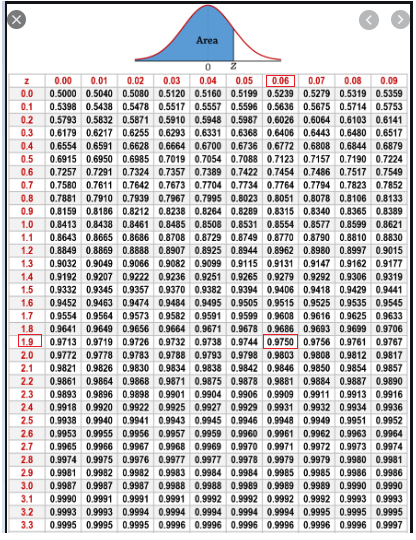
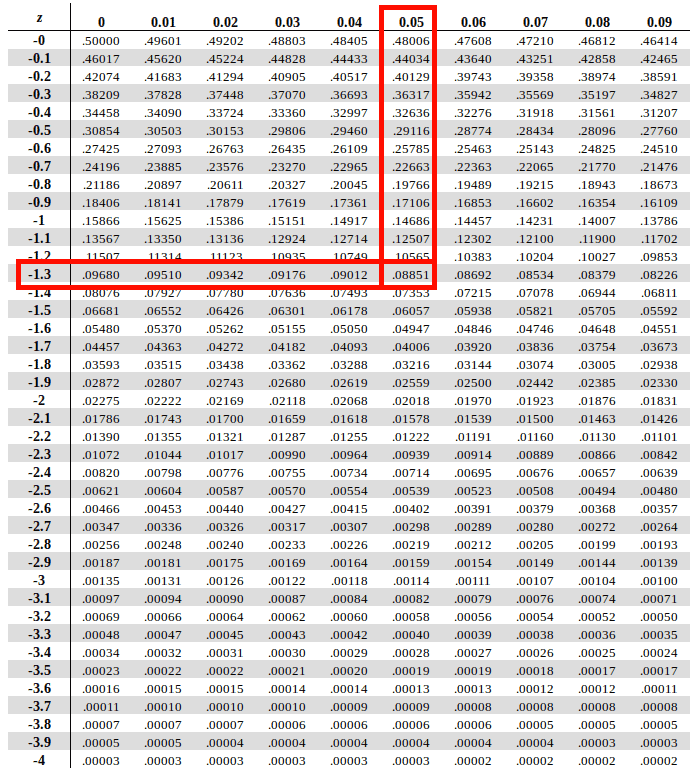
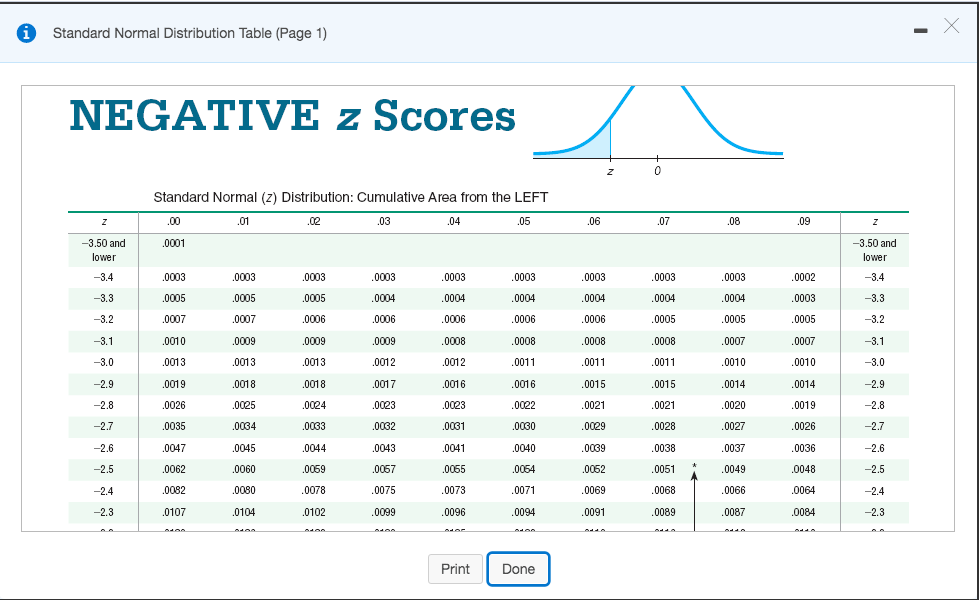
A z-score is measured in units of the standard deviation. Simply put, if an examiner asks you to find the probability behind a given positive z-value, you will have to look it up directly on the table, knowing that \(P(Z ≤ z) = θ(z)\) when \(z\) is positive. The standard normal distribution is a normal distribution of standardized values called z-scores.
However, the table does this only when we have positive values of \(z\). Using the standard normal distribution table, we can confirm that a normally distributed random variable \(Z\), with a mean equal to 0 and variance equal to 1, is less than or equal to \(z\), i.e., \(P(Z ≤ z)\).